Las leyes fundamentales están sujetas a los principios de la Mecánica Cuántica. Esta teoría es uno de los mayores descubrimientos hechos por el hombre, pero es también uno de los más difíciles de comprender por la mente humana porque va contra nuestra intuición.
El universo consta de materia compuesta de partículas elementales como los electrones y los fotones. Las partículas carecen de individualidad (cada electrón del universo es idéntico a cualquier otro y todos los fotones son intercambiables). Sin embargo cada partícula puede ocupar uno entre un número infinito de estados cuánticos.
Hay dos grandes grupos de partículas: los fermiones que obedecen el principio de exclusión de Pauli, y los bosones, que tienen tendencia a ocupar el mismo estado al mismo tiempo.
Por eso los bosones pueden aumentar su densidad hasta tener un comportamiento prácticamente clásico, como el de los campos electromagnéticos y gravitatorio. Las partículas bosónicas pueden considerarse en este caso como los cuantos de estos campos.
De hecho todas las fuerzas fundamentales deben estar asociadas a una partícula elemental, el cuanto o bosón del campo correspondiente.
Los fermiones pueden describirse también en términos de campos, que aunque no se comportan en absoluto de manera clásica, pueden sin embargo asociarse, en cierto sentido, con fuerzas.
La materia está formada por electrones, protones y neutrones sencillamente porque todas las demás partículas masivas son muy inestables a las energías normales de nuestro mundo.
Toda teoría sobre las partículas elementales se desarrrolla dentro del marco de la teoría cuántica de campos, que incluye tanto el modelo estándar como la teoría del núcleo. Está basada en tres supuestos fundamentales:
- La validez de la mecánica cuántica.
- La validez del principio de relatividad de Einstein.
- La localidad, es decir, todas las fuerzas fundamentales surgen de procesos locales y no de la acción a distancia. Estos procesos locales incluyen la emisión y absorción de partículas.
La comprensión de por qué las ecuaciones de la mecánica cuántica son las que son, de por qué la materia esta formada por unas partículas determinadas y de por qué existe algo como la luz vino con el éxito del modelo estándar de partículas. Un requisito clave para ello fue la reconciliación en los años 40 de la Relatividad Especial con la mecánica cuántica. Ambas son prácticamente incompatibles y solo pueden coexistir en un tipo determinado de teorías. En estas teorías las fuerzas entre partículas solo pueden surgir del intercambio de otras partículas. Además todas estas partículas son cuantos de varios tipos de campos. Por ejemplo existe un campo electrónico cuyo cuanto es el electrón y el cuanto del campo electromagnético es el fotón. No existen campos para los protones y los neutrones porque estos están formados por otras partículas elementales: los quarks, que sí tienen campos asociados.
Por eso las ecuaciones de una teoría de campos como el modelo estándar no tratan con partículas sino con campos: las partículas aparecen como manifestaciones o excitaciones de dichos campos.
El universo consta de materia compuesta de partículas elementales como los electrones y los fotones. Las partículas carecen de individualidad (cada electrón del universo es idéntico a cualquier otro y todos los fotones son intercambiables). Sin embargo cada partícula puede ocupar uno entre un número infinito de estados cuánticos.
Hay dos grandes grupos de partículas: los fermiones que obedecen el principio de exclusión de Pauli, y los bosones, que tienen tendencia a ocupar el mismo estado al mismo tiempo.
Por eso los bosones pueden aumentar su densidad hasta tener un comportamiento prácticamente clásico, como el de los campos electromagnéticos y gravitatorio. Las partículas bosónicas pueden considerarse en este caso como los cuantos de estos campos.
De hecho todas las fuerzas fundamentales deben estar asociadas a una partícula elemental, el cuanto o bosón del campo correspondiente.
Los fermiones pueden describirse también en términos de campos, que aunque no se comportan en absoluto de manera clásica, pueden sin embargo asociarse, en cierto sentido, con fuerzas.
El Modelo Estándar de la Física de Partículas
El Modelo Estándar es una Teoría Cuántica de Campos que consiste en las fuerzas que no son la fuerza gravitatoria y las partículas que experimentan estas fuerzas. Además de la muy conocida fuerza del electromagnetismo, hay otras dos fuerzas que actúan dentro del núcleo: la fuerza fuerte y la fuerza débil.
La fuerza débil plantea el misterio más importante que queda sin resolver sobre el Modelo Estándar. Mientras en las partículas que comunican las otras dos fuerzas son partículas sin masa, los bosones gauge que comunican la fuerza débil, sí que tienen masa.
Además de las partículas que comunican fuerzas (el fotón, el gravitón, el gluón y los bosones gauge débiles) el Modelo Estándar contiene partículas que experimentan esas fuerzas. Estas partículas se dividen en dos categorías: los quarks, que experimentan la fuerza fuerte, y los leptones, que no la experimentan.
Los quarks y los leptones ligeros que se encuentran en la materia (quark up, quark down y el electrón) no son las únicas partículas conocidas. También existen quarks y leptones más pesados: el quark up, el quark down y el electrón tienen todos dos versiones más pesadas. Además todas estas partículas tienen sus correspondientes antipartículas. En el caso del electrón, sería el positrón.
Los bariones son hadrones formados por la unión de 3 quarks mientras que los mesones son hadrones formados por un quark y un antiquark
Estas partículas pesadas son inestables, lo cual quiere decir que se desintegran generando quarks y leptones más ligeros. Pero experimentos que se han llevado a cabo en los aceleradores de partículas las han producido y han demostrado que estas partículas más pesadas experimentan las mismas fuerzas que las familiares y ligeras partículas estables.
La materia está formada por electrones, protones y neutrones sencillamente porque todas las demás partículas masivas son muy inestables a las energías normales de nuestro mundo.
En el Tevatrón del Fermilab se descubrió el quark top en 1995. Esta es una de las últimas confirmaciones del Modelo Estándar.
Familias de fermiones
Los quarks, electrones, neutrinos y sus antipartículas se agrupan en tres familias. Cada una de ellas con un electrón o partícula análoga a él (muón y tau), un neutrino y dos sabores de quarks de tres colores.
Las partículas elementales del Modelo Estándar se agrupan en 3 familias de dos quarks y dos leptones cada una. En esta imagen cada familia corresponde a las partículas de las primeras dos columnas de la izquierda, las dos columnas centrales y las dos columnas de la derecha
Asociados al color encontramos los gluones de la QCD y, al sabor, estan los cuatro bosones gauge de la interacción electrodébil: el fotón, los W± y Z°.
En principio no hay más familias fermiónicas que estas tres. Las predicciones de la desintegración de Z° comprobadas experimentalmente permiten su desintegración en tres clases de pares neutrino-antineutrino, correspondientes precisamente a los neutrinos electrónico, muónico y tauónico. No hay lugar para una cuarta clase de neutrino, a menos que tenga una masa gigantesca.
Dispersión de un neutrino electrónico en un quark down
La física que conocemos puede sintetizarse de manera asombrosa en una ecuación "maestra". Se trata de una densidad Lagrangiana o "Lagrangiana". A partir de esta Lagrangiana, el principio de mínima acción y aplicando el cálculo de variaciones mediante las ecuaciones de Euler-Lagrange pueden obtenerse las ecuaciones del movimiento para cada situación física concreta.
Lagrangiana del Modelo Estándar
Lagrangiana completa del Modelo Estándar de Partículas donde h.c. quiere decir hermítico conjugado.
Esta ecuación "maestra" constituye el núcleo del Modelo Estándar y especifica las reglas según las cuales interactúan entre sí dos partículas cualesquiera en cualquier lugar del Universo, salvo las de la gravedad.
La ecuación maestra muestra una gran elegancia y sencillez y una gran belleza subyacente. Además especifica las propiedades de las tres fuerzas con todo detalle, con precisión matemática y sin ambigüedad ni redundancia. Estaría compuesta por 4 partes:
LTotal=LMateria+LGauge+LYukawa+LHiggs
Teoría de Dirac
La primera línea es la lagrangiana de Dirac a partir de la que se obtiene la Ecuación de Dirac, que es el punto de partida de las Teorías Cuánticas de Campos en general y de la Electrodinámica Cuántica en particular.
La primera línea es la lagrangiana de Dirac a partir de la que se obtiene la Ecuación de Dirac, que es el punto de partida de las Teorías Cuánticas de Campos en general y de la Electrodinámica Cuántica en particular.

Ecuación de Dirac inscrita en el sepulcro del gran físico Paul Dirac
La segunda línea nos dice como interactúa el fotón (y el bosón gauge débil Z°) con la materia (primer término donde la letra griega psi indica una partícula de materia) y consigo mismo (segundo término).

Estas dos primeras líneas son muy parecidas a la lagrangiana de la Electrodinámica Cuántica, teoría que explica cómo interaccionan la luz y la materia y que modifican ligeramente las Ecuaciones de Maxwell para dar cuenta de efectos sutiles.

Las dos primeras líneas de la Ecuación Maestra son muy parecidas a la lagrangiana de la Electrodinámica Cuántica. La diferencia está en el tensor B que aquí incorpora el bosón gauge débil Zº.
Estas dos primeras líneas son muy parecidas a la lagrangiana de la Electrodinámica Cuántica, teoría que explica cómo interaccionan la luz y la materia y que modifican ligeramente las Ecuaciones de Maxwell para dar cuenta de efectos sutiles.
Lagrangiana de la Electrodinámica Cuántica, la teoría que describe como interacciona la luz con la materia. M es la masa del electrón, A es el potencial vector del electromagnetismo y F es el tensor electromagnético. Los dos primeros términos corresponden a la ecuación de Dirac, el tercero es el de interacción entre el electrón y el fotón (consecuencia de la simetría gauge) y el cuarto es el de la propagación del fotón en ausencia de fuentes (onda electromagnética)
Salvo la gravedad, en estas dos primeras líneas están todas las leyes fundamentales de la física que conocemos, como las Ecuaciones de Maxwell o la Teoría de la Relatividad Especial de Einstein.
Esta emisión y absorción podría parecer que viola el principio de conservación de la energía o el momento. Pero en mecánica cuántica esto puede suceder dentro de los límites del principio de Incertidumbre.
El sistema puede tomar prestada por un momento un poco de energía para permitir que el primer electrón emita un fotón, energía que será devuelta cuando el otro electrón lo absorba. Esto se conoce como un intercambio virtual de un fotón entre dos electrones.
La teoría de Dirac era un ingrediente clave de la electrodinámica cuántica en los años 30 y 40. Además predijo el espín del electrón y la antimateria (en 1932 se descubrió el positrón). Pero hoy sabemos que el punto de vista de Dirac era equivocado pues el contexto adecuado para la reconciliación de la mecánica cuántica con la relatividad especial es el formalismo conocido como teoría cuántica de campos, presentada por Heisenberg y Pauli en 1929 donde todas las partículas son cuantos de su campo asociado.
En cualquier teoría cuántica de campos pueden usarse los diagramas de Feynman que simplifican los cálculos de probabilidades.
La electrodinámica cuántica permitía calcular correctamente una amplia variedad de procesos físicos:
A mediados de los años 30 sin embargo tenía un problema de consistencia interna cuando se aplicaba a casos de energía elevadas: el problema de los infinitos.
Este problema se manifestó claramente en un artículo de Julius Robert Oppenheimer de 1930 donde intentaba calcular un sutil desplazamiento de la energía de un átomo debido a la emisión y reabsorción de un fotón (virtual) por un electrón sin que ninguno de ellos abandone el átomo. Según el procedimiento de la electrodinámica cuántica, este proceso produce un desplazamiento de la energía del átomo calculable como la suma de infinitas contribuciones, una por cada posible energía del fotón. Esta suma debería ser finita, pero resulta infinita aunque los experimentos muestran que obviamente no lo es.
En 1947 Willis Lamb midió el tipo de efecto que Oppenheimer había intentado calcular en 1930: un desplazamiento de la energía del átomo de hidrógeno debido a la emisión y reabsorción de fotones.
Esta energía total depende de la masa desnuda y la carga desnuda del electrón, la masa y la carga que aparecen en la teoría antes de que empecemos a preocuparnos por la emisión y la reabsorción de fotones. Pero los electrones libres, al igual que los electrones en los átomos, siempre están emitiendo y reabsorbiendo fotones que afectan a la masa y la carga del electrón y, por consiguiente, la masa y la carga desnudas no son las mismas que la masa y la carga medidas del electrón. Para explicar los valores observados (finitos) de la masa y la carga del electrón, la masa y la carga desnudas deben ser infinitas.
La energía total del átomo es, por tanto, la suma de dos términos, ambos infinitos: la energía desnuda, que es infinita, y el desplazamiento de la energía de Oppenheimer que también es infinito porque recibe contribuciones de fotones virtuales de energía ilimitada.
Sin embargo Oppenheimer había omitido algo en su cálculo: las contribuciones al desplazamiento de energía de procesos en los que un positrón, un fotón y un segundo electrón surgen espontáneamente del espacio vacío para que, a continuación, el fotón sea absorbido en la aniquilación del positrón y del electrón original. Este extraño proceso debe ser incluido para que la energía del átomo dependa de la velocidad tal y como exige la relatividad especial.
Si se considera el proceso positrónico y las diferencias entre las cargas y masas desnudas del electrón y sus valores medidos, entonces parecía que se podían cancelar los infinitos en el desplazamiento de energía.
Poco después se refinaron los cálculos incluyendo todos los efectos relativistas y los infinitos se cancelaron sin necesidad de simplificaciones arbitrarias.
La electrodinámica cuántica fue salvada mediante la idea de la cancelación de los infinitos en una redefinición o renormalización de la carga y la masa del electrón.
Pero el problema de los infinitos puede ser resuelto solo si estos aparecen de una manera concreta, lo que ocurre únicamente en un número limitado de teorías cuánticas de campos especialmente simples llamadas renormalizables. La versión más simple de la electrodinámica cuántica es renormalizable y eso explica por qué es como es. Cualquier pequeño cambio haría que fuera inconsistente y que los infinitos no pudieran cancelarse.
Aún así los calculos eran tremendamente complicados y con sumas cuyos términos individuales eran incompatibles com la relatividad especial. Mientras Feynman, Schwinger y Tomonaga estaban desarrollando métodos de cálculo más sencillos y compatibles con la relatividad especial en todos sus pasos.
Utilizaron estos métodos para realizar otros cálculos en asombroso acuerdo con los experimentos, como el del momento magnético del electrón. En 1928 Dirac realizo este cálculo cuyo valor fue corregido en 1,00115965214 (valor medido 1,00115965218±4 en la última cifra decimal) considerando la emisión y reabsorción de fotones virtuales y otros efectos. Es posiblemente el caso más espectacular de acuerdo numérico entre teoría y experimento.
Electrodinámica Cuántica
Es el primer ejemplo de teoría cuántica de campos satisfactoria cuyo origen está en la ecuación relativista del electrón publicada por Dirac en 1928. Es la teoría del electrón y el fotón. En el marco de esta teoría, la fuerza electromagnética entre dos electrones surge de la emisión de un fotón por una de las partículas y su absorción por la otra.
La ecuación de Dirac del electrón
Esta emisión y absorción podría parecer que viola el principio de conservación de la energía o el momento. Pero en mecánica cuántica esto puede suceder dentro de los límites del principio de Incertidumbre.
El Principio de Incertidumbre de Heisenberg
El sistema puede tomar prestada por un momento un poco de energía para permitir que el primer electrón emita un fotón, energía que será devuelta cuando el otro electrón lo absorba. Esto se conoce como un intercambio virtual de un fotón entre dos electrones.
La teoría de Dirac era un ingrediente clave de la electrodinámica cuántica en los años 30 y 40. Además predijo el espín del electrón y la antimateria (en 1932 se descubrió el positrón). Pero hoy sabemos que el punto de vista de Dirac era equivocado pues el contexto adecuado para la reconciliación de la mecánica cuántica con la relatividad especial es el formalismo conocido como teoría cuántica de campos, presentada por Heisenberg y Pauli en 1929 donde todas las partículas son cuantos de su campo asociado.
En cualquier teoría cuántica de campos pueden usarse los diagramas de Feynman que simplifican los cálculos de probabilidades.
Los diagramas de Feynman son la herramienta principal de la Electrodinámica Cuántica. Su uso facilita enormemente los cálculos. En este caso un positrón y un electrón se aniquilan mutuamente en un fotón que luego se divide nuevamente en un positrón y un electrón.
La teoría cuántica de campos implica una simetría fundamental entre las partículas elementales y sus antipartículas. Para cada partícula hay una antipartícula correspondiente con su misma masa pero carga opuesta, que se comporta como la partícula pero moviéndose hacia atrás en el tiempo y en el espacio. La antipartícula de la antipartícula es la propia partícula. La antipartícula del electrón es el positrón y del fotón es ella misma.
La electrodinámica cuántica permitía calcular correctamente una amplia variedad de procesos físicos:
- La dispersión de un fotón que colisiona con un electrón.
- La dispersión de un electrón por otro.
- La aniquilación o producción de un electrón y positrón.
A mediados de los años 30 sin embargo tenía un problema de consistencia interna cuando se aplicaba a casos de energía elevadas: el problema de los infinitos.
Este problema se manifestó claramente en un artículo de Julius Robert Oppenheimer de 1930 donde intentaba calcular un sutil desplazamiento de la energía de un átomo debido a la emisión y reabsorción de un fotón (virtual) por un electrón sin que ninguno de ellos abandone el átomo. Según el procedimiento de la electrodinámica cuántica, este proceso produce un desplazamiento de la energía del átomo calculable como la suma de infinitas contribuciones, una por cada posible energía del fotón. Esta suma debería ser finita, pero resulta infinita aunque los experimentos muestran que obviamente no lo es.
En 1947 Willis Lamb midió el tipo de efecto que Oppenheimer había intentado calcular en 1930: un desplazamiento de la energía del átomo de hidrógeno debido a la emisión y reabsorción de fotones.
El desplazamiento de la energía de un átomo debido a la emisión y reabsorción de fotones no es realmente un observable. El único observable es la energía total del átomo, que se calcula añadiendo este desplazamiento de energía a la energía calculada por Dirac en 1928.
Esta energía total depende de la masa desnuda y la carga desnuda del electrón, la masa y la carga que aparecen en la teoría antes de que empecemos a preocuparnos por la emisión y la reabsorción de fotones. Pero los electrones libres, al igual que los electrones en los átomos, siempre están emitiendo y reabsorbiendo fotones que afectan a la masa y la carga del electrón y, por consiguiente, la masa y la carga desnudas no son las mismas que la masa y la carga medidas del electrón. Para explicar los valores observados (finitos) de la masa y la carga del electrón, la masa y la carga desnudas deben ser infinitas.
La energía total del átomo es, por tanto, la suma de dos términos, ambos infinitos: la energía desnuda, que es infinita, y el desplazamiento de la energía de Oppenheimer que también es infinito porque recibe contribuciones de fotones virtuales de energía ilimitada.
Sin embargo Oppenheimer había omitido algo en su cálculo: las contribuciones al desplazamiento de energía de procesos en los que un positrón, un fotón y un segundo electrón surgen espontáneamente del espacio vacío para que, a continuación, el fotón sea absorbido en la aniquilación del positrón y del electrón original. Este extraño proceso debe ser incluido para que la energía del átomo dependa de la velocidad tal y como exige la relatividad especial.
Este es un ejemplo del resultado encontrado previamente por Dirac de que la mecánica cuántica solo es compatible con la relatividad especial si se consideran las antipartículas como el positrón.
Si se considera el proceso positrónico y las diferencias entre las cargas y masas desnudas del electrón y sus valores medidos, entonces parecía que se podían cancelar los infinitos en el desplazamiento de energía.
Poco después se refinaron los cálculos incluyendo todos los efectos relativistas y los infinitos se cancelaron sin necesidad de simplificaciones arbitrarias.
La electrodinámica cuántica fue salvada mediante la idea de la cancelación de los infinitos en una redefinición o renormalización de la carga y la masa del electrón.
Pero el problema de los infinitos puede ser resuelto solo si estos aparecen de una manera concreta, lo que ocurre únicamente en un número limitado de teorías cuánticas de campos especialmente simples llamadas renormalizables. La versión más simple de la electrodinámica cuántica es renormalizable y eso explica por qué es como es. Cualquier pequeño cambio haría que fuera inconsistente y que los infinitos no pudieran cancelarse.
Aún así los calculos eran tremendamente complicados y con sumas cuyos términos individuales eran incompatibles com la relatividad especial. Mientras Feynman, Schwinger y Tomonaga estaban desarrollando métodos de cálculo más sencillos y compatibles con la relatividad especial en todos sus pasos.
Lagrangiana de la Electrodinámica Cuántica, la teoría que describe como interacciona la luz con la materia. M es la masa del electrón, A es el potencial vector del electromagnetismo y F es el tensor electromagnético. Los dos primeros corresponden a la ecuación de Dirac, el tercero es el de interacción entre el electrón y el fotón (consecuencia de la simetría gauge) y el cuarto es el de la propagación del fotón en ausencia de fuentes (onda electromagnética)
Utilizaron estos métodos para realizar otros cálculos en asombroso acuerdo con los experimentos, como el del momento magnético del electrón. En 1928 Dirac realizo este cálculo cuyo valor fue corregido en 1,00115965214 (valor medido 1,00115965218±4 en la última cifra decimal) considerando la emisión y reabsorción de fotones virtuales y otros efectos. Es posiblemente el caso más espectacular de acuerdo numérico entre teoría y experimento.
Sin embargo la QED no explica:
- Los procesos debidos a la fuerza nuclear fuerte que mantienen unidos a los quarks en protones y neutrones.
- Procesos relacionados con la fuerza nuclear débil, responsable de la fusión nuclear.
Ambas fuerzas están descritas por la misma aproximación basada en Teoría Cuántica de Campos que la descrita para la QED: la teoría electrodébil y la cromodinámica cuántica. La teoría de estas 3 fuerzas en su conjunto se conoce como Modelo Estándar.
Teoría Electrodébil
La tercera línea nos dice como interactúan los bosones gauge débiles (W+, W- y el fotón) con la materia (primer término) y consigo mismos (segundo término). Estas tres primeras líneas constituyen la lagrangiana de la Teoría Electrodébil, que unifica el electromagnetismo con la fuerza nuclear débil.
Línea de la Ecuación Maestra que indica la interacción de los bosones gauge débiles con la materia y consigo mismos
Electrón y neutrino electrónico
Los electrones no poseen color pero sí sabor. El electrón tiene como compañero el neutrino electrónico, que además de no tener color tampoco tiene carga eléctrica. Unido a su minúscula masa, es una partícula que apenas interacciona.
La mayoria de los neutrinos que atraviesan la Tierra se generan en las reacciones termonucleares, o de fusión nuclear, en el interior del Sol a través de la fuerza débil.
La desintegración radiactiva beta está gobernada por la fuerza débil. En ella un neutrón se convierte en un protón, un electrón y un antineutrino
Un electrón se transforma en un neutrino electrónico a la vez que un quark up se convierte en un quark down. Dos versiones del mismo diagrama de Feynman
En estas reacciones se produce un cambio de sabor tanto en el electrón que se convierte en un neutrino electrónico (y viceversa) como del quark up que se convierte en un quark down (y viceversa).
Como en toda interacción descrita por una teoría cuántica de campos, esta es mediada por un cuanto. En estos casos son los bosones gauge débiles W±.
Fuerza Nuclear Débil
Esta fuerza juega un papel esencial en las cadenas de reacciones nucleares que generan energía y producen los diferentes elementos químicos en los núcleos de las estrellas.
Esta fuerza quedó de manifiesto por primera vez en el descubrimiento de la radiactividad por Henri Becquerel en 1896. La radiación beta origen de esta radiactividad consiste en que un neutrón se convierta en un protón a la vez que se crea un electrón y un antineutrino que son expulsados del núcleo. Este cambio de identidad de las partículas es algo que no está permitido por ninguna otra fuerza de las conocidas anteriormente.
La fuerza nuclear débil es mucho menos intensa que las fuerzas electromagnética o nuclear fuerte. Esto queda de manifiesto en que es una fuerza lenta ya que cualquier proceso en el que interviene dura una centésima de segundo, cuando la nuclear fuerte necesita solo 10-24s. Otra característica peculiar es que presenta una asimetría izquierda-derecha o quiralidad.
En 1967, Steven Weinberg desarrolló una base matemática para una teoría de la fuerza nuclear débil muy potente que posibilitaba una teoría de esta fuerza análoga a la electrodinámica cuántica. Igual que la fuerza electromagnética actúa mediante el intercambio de fotones, una fuerza débil no actuaría instantáneamente y en un único punto del espacio, sino que sería producida por el intercambio de bosones entre partículas distantes. Estos bosones debían tener masa porque sino ya se hubieran descubierto. Pero como operaban de manera tan similar al fotón en la electrodinámica cuántica que parecía que la teoría también sería renormalizable mediante redefinición de masas y otras magnitudes. Además esta teoría era muy determinada por sus principios subyacentes evitando la arbitrariedad.
Diagrama de Feynman de la desintegración beta en la que un quark down se convierte en un quark up emitiendo un bosón W- que luego se desintegra en un electrón y un antineutrino
Más allá de una analogía de la electrodinámica cuántica, esta teoría resultaba ser una teoría unificadora de las fuerzas nuclear débil y electromagnética, siendo ambas aspectos diferentes de la fuerza electrodébil. El fotón se unía a los bosones gauge débiles W± (responsables de la radiación beta) y Z° (responsable de un tipo neutro de fuera débil conocida como corriente neutra débil). La misma teoría en esencia fue desarrollada independientemente por Abdus Salam y Sheldon Glashow en 1968.
Diagramas de Feynman de corrientes neutras débiles en las que no hay intercambio de carga
Tanto Weinberg como Salam creían que esta teoría era renormalizable pero no fueron capaces de demostrarlo. Fue Gerard t'Hooft en 1971 quien lo consiguió utilizando un novedoso método matemático desarrollado por Feynman. A partir de este momento y del descubrimiento en 1973 de las corrientes neutras predichas por la teoría electrodébil en experimentos de dispersión de neutrinos la teoría electrodébil empezó a ser considerada seriamente gracias también a su consistencia y rigidez interna.
Las verificaciones más espectaculares de la teoría electrodébil fueron los experimentos llevados a cabo por el equipo de Carlo Rubbia en el CERN en 1983 con el descubrimiento de las partículas W y en 1984 con la partícula Z con las propiedades predichas por la teoría electrodébil.
Igual que con la Relatividad General o la electrodinámica cuántica, la teoría electrodébil tuvo un consenso a favor previo a la confirmación experimental debido a su belleza (simplicidad, inevitabilidad y consistencia interna).
Dinámica cuántica del sabor y corrientes neutras
Tanto el electromagnetismo como las interacciones débiles pueden considerarse fuerzas de sabor. Por ello no es de extrañar que se unificaran bajo la teoría electrodébil. Uno de los primeros éxitos de esta teoría fue predecir el bosón gauge débil eléctricamente neutro Z°, mediador de una fuerza de sabor que causa la dispersión de los neutrinos electrónicos por parte de protones y neutrones sin cambio de sabor.
Cuarta línea de la ecuación maestra
La cuarta línea nos dice como interactúan los gluones con los quarks (primer término) y consigo mismos (segundo término). Esta cuarta línea constituye la lagrangiana de la Cromodinámica Cuántica, que es la Teoría Cuántica de Campos que describe la fuerza nuclear fuerte.
Línea de la Ecuación Maestra que indica la interacción de los gluones con los quarks y consigo mismos
Cromodinámica cuántica
Es la teoría cuántica de campos definida para quarks y gluones.
Quarks
Los compañeros del electrón en el átomo, el protón y el neutrón, son partículas compuestas por tres quarks cada una. En el caso del protón dos quarks up y uno down. Y el neutrón agrupa dos quarks down y uno up. El quark up tiene carga 2/3 y el quark down -1/3 para así obtener la carga +1 del protón y la carga neutra del neutrón.
Se dice que up y down son diferentes sabores de quark. Los quarks tienen además otra propiedad aún más importante llamada color. Para formar un protón o un neutrón los tres quarks deben tener colores diferentes (rojo, verdela y azul) de manera que estos sean blancos.
Quarks confinados
Los quarks tienen la notable propiedad de estar permanentemente atrapados dentro de partículas blancas como el protón y el neutrón. Solo las partículas blancas son directamente observables en el laboratorio. Solo en su interior pueden existir objetos coloreados. De la misma forma, la carga eléctrica de una partícula observable es siempre un número entero, y las partículas con carga fraccionaria sólo pueden existir en su interior.
Es la teoría cuántica de campos definida para quarks y gluones.
Quarks
Los compañeros del electrón en el átomo, el protón y el neutrón, son partículas compuestas por tres quarks cada una. En el caso del protón dos quarks up y uno down. Y el neutrón agrupa dos quarks down y uno up. El quark up tiene carga 2/3 y el quark down -1/3 para así obtener la carga +1 del protón y la carga neutra del neutrón.
Se dice que up y down son diferentes sabores de quark. Los quarks tienen además otra propiedad aún más importante llamada color. Para formar un protón o un neutrón los tres quarks deben tener colores diferentes (rojo, verdela y azul) de manera que estos sean blancos.
Quarks confinados
Los quarks tienen la notable propiedad de estar permanentemente atrapados dentro de partículas blancas como el protón y el neutrón. Solo las partículas blancas son directamente observables en el laboratorio. Solo en su interior pueden existir objetos coloreados. De la misma forma, la carga eléctrica de una partícula observable es siempre un número entero, y las partículas con carga fraccionaria sólo pueden existir en su interior.
Gluones coloreados
Los quarks interaccionan entre sí por una fuerza que surge del intercambio virtual de gluones. Estos bosones son indiferentes al sabor pero muy sensibles al color. Para ellos, el color es similar a lo que es la carga eléctrica para los fotones.
La triple naturaleza del color requiere de los gluones una propiedad que no comparten con el fotón: existen diferentes gluones para las diferentes interacciones de color.
Por ejemplo, un quark rojo se convierte en azul emitiendo un gluon virtual rojo-azul, el cual es absorbido por un quark azul que se convierte a su vez en rojo. La antipartícula del gluón rojo-azul es un gluón azul-rojo.
Comparación entre la QCD y la QED. Los quarks y antiquarks se asocian con el fotón a través de su carga eléctrica, pero el positrón y el electrón no se asocian con los gluones
Intercambio de fotones virtuales y gluones virtuales
La fuente de la fuerza electromagnética son las cargas eléctricas. En el caso de la fuerza de color, esta surge de las cargas de color.
No obstante existe una diferencia crucial entre ambas teorías: el fotón es eléctricamente neutro mientras que los gluones estan coloreados. Esto hace que los gluones interactúen entre sí de una manera imposible para los fotones, lo que origina términos en las ecuaciones de la QCD que no tienen analogo en la QED.
La fuerza de color se comporta de manera muy distinta a la electromagnética o cualquier otra fuerza conocida: no se desvanece a largas distancias. Esta propiedad explica el confinamiento de quarks, antiquarks y gluones en objetos blancos como protones y neutrones. Otra propiedad de esta fuerza es la libertad asintótica, que hace que su intensidad se reduzca a medida que la distancia entre quarks se reduce, anulándose para distancias tendiendo asintóticamente a cero.
La simplicidad revelada por la QCD
La fuerza nuclear que liga (pero no confina) a protones y neutrones en el núcleo no es fundamental, sino que surge como un efecto secundario de la fuerza de color, que a su vez procede de la interaccion entre quarks y gluones. Esto es similar a lo que ocurre con las fuerzas entre átomos o moléculas. Estas fuerzas tampoco son fundamentales, sino una consecuencia indirecta de la cuantización de la fuerza electromagnética.
Además del protón y del neutrón hay multitud de partículas blancas (como el barión lambda) que gracias a la QCD son explicadas como combinaciones de quarks, antiquarks y gluones. La QCD ha revelado así una simplicidad subyacente a una complejidad aparente.
Los bariones protón, neutrón y lambda formados por tres quarks y los mesones (formados por un par quark-antiquark) son ejemplos de las dos familias de hadrones
Por otra parte, todas las partículas formadas por quarks interaccionan entre sí a través de la interacción fuerte, que incluye la fuerza nuclear. Esta interacción es consecuencia indirecta de la interacción fundamental quark-gluón.
Fuerzas entre quarks a partir del intercambio de dos gluones virtuales
Simetrías
Un principio de simetría es simplemente una afirmación de que algo se ve igual desde varios puntos de vista, como por ejemplo una esfera o el espacio vacío. Pero lo realmente importante no son las simetrias de las cosas, sino las simetrías de las leyes o principios de invariancia. En general, las leyes de la naturaleza son simétricas o invariantes respecto a la traslación y la rotación espacial o a la traslación temporal. El principio de relatividad de la teoría de la relatividad también es una simetría de la naturaleza. Cualquier principio de simetría es a su vez un principio de simplicidad. Si estas simetrías de las leyes de la naturaleza son importantes en física clásica, su importancia es aún mayor en mecánica cuántica.
Un electrón es idéntico a cualquier otro salvo en su energía, momento y espín. Estas magnitudes son las que caracterizan las formas en que la función de onda responde a transformaciones de simetría. La materia pierde así su papel central en física.
Hoy día se acepta generalmente que la única forma de combinar los principios de la relatividad especial y la mecánica cuántica es a través de una teoría cuántica de campos o algo muy similar. Este es precisamente el tipo de rigidez lógica que da su belleza a una teoría realmente fundamental: la mecánica cuántica y la relatividad especial son casi incompatibles, y su reconciliación en la teoría cuántica de campos impone poderosas restricciones a la forma en que las partículas pueden interaccionar mutuamente.
Una de estas restricciones es que se difumina la diferencia entre campos y partículas. Todo son campos y las partículas son manifestaciones o excitaciones de los campos allí donde su energía es suficiente para crearlas. Y en el caso de las partículas virtuales, ni eso porque gracias al principio de incertidumbre pueden tomar prestada la energía del vacío durante un tiempo suficientemente pequeño. De hecho así funcionan las interacciones, mediante el inintercambio de partículas virtuales.
En el caso del campo electromagnético, la interacción entre dos electrones es debida al intercambio de fotones y la interacción entre un electrón y un fotón por el intercambio de electrones (campo electrónico). La distinción entre materia y fuerza deja de ser esencial porque las partículas de materia también pueden transmitir fuerzas.
Otra de estas restricciones es que la energía y el momento de los campos esta cuantizada. Por ejemplo, en el campo gravitatorio la energía es transportada por los gravitones.
Todas las teorías mencionadas hasta ahora solamente limitan los tipos de fuerzas y materia que una teoría puede contener: en sí mismas no requieren la existencia de ningún tipo particular de materia o fuerza. Los principios de simetría se han vuelto cruciales en las últimas décadas del siglo XX: hay principios de simetría que dictan la existencia misma de todas las fuerzas conocidas de la naturaleza.
La simetría subyacente en la teoría electrodébil no es espacio-temporal sino que tiene que ver con la identidad de las partículas. En mecanica cuántica es posible tener una partícula que no es, por ejemplo, ni un electrón ni un neutrino hasta que no se mida una propiedad que las distinga como la carga eléctrica. En la teoría electrodébil, la forma de las leyes de la naturaleza permanece invariable si reemplazamos electrones y neutrinos por estados combinados de ambos.
Esta es la simetría que conecta las fuerzas electromagnéticas con las fuerzas nucleares débiles. El fotón y las partículas W± y Z aparecen en la teoría electrodébil como paquetes de energía de cuatro campos, campos que son requeridos por esta simetría de la teoría electrodébil de igual forma que el campo gravitatorio es requerido por las simetrías de la relatividad general.
Estas simetrías se denominan simetrías internas porque estan relacionadas con la naturaleza intrínseca de las partículas más que con su posición o movimiento. La invariancia de las leyes de la naturaleza bajo un grupo de tales transformaciones de simetría interna dependientes de la posición y el tiempo se denomina simetría local o gauge.
Es la simetría local entre diferentes sistemas de referencia en el espacio y en el tiempo lo que hace necesaria la gravitación y, análogamente, es una segunda simetría local entre electrones y neutrinos lo que hace necesaria la existencia del campo fotónico, del campo W y del campo Z.
Todavía existe una tercera simetría local exacta asociada con la propiedad interna de los quarks conocida como carga de color. Cada uno de los 6 tipos o sabores de quarks se da en tres colores: rojo, blanco y azul. Pues existe una simetría exacta de la naturaleza entre los diferentes colores. La fuerza entre un quark rojo y uno blanco es la misma que entre un quark blanco y uno azul, y la fuerza entre dos quarks rojos es la misma que entre dos quarks azules.
Pero esta simetría va más allá del mero intercambio de colores. En mecánica cuántica podemos considerar estados de un solo quark que no son ni exactamente rojos ni exactamente blancos ni exactamente azules. Las leyes de la naturaleza toman exactamente la mismisma forma si reemplazamos los quarks rojos, blanco y azul por quarks en tres combinaciones de estados apropiada.
El hecho de que las leyes de la naturaleza no se vean afectadas al variar de un lugar a otro y de un instante a otro hace necesario incluir en la teoría una familia de campos que interaccionan con los quarks, análogos al campo gravitatorio. Son ocho campos que se conocen como campos gluónicos. La teoría de tales fuerzas, la cromodinámica cuántica, es sencillamente la teoría de quarks y gluones que respeta esta simetría de color local. El modelo estándar de las partículas elementales consiste en la teoría electrodébil ccombinada com la cromodinámica cuántica.
No solo los principios de simetría dan una especie de rigidez o inevitabilidad a las teorías. Únicamente con estos principios la teoría electrodébil o la cromodinámica cuántica serían solo uno de los muchos tipos de teorías posibles. La restricción adicional que nos permite escoger nuestro modelo estándar sencillo de entre la variedad de teorías más complicadas que satisfacen los mismos principios de simetría es que sea renormalizable. Resulta que esta condición impone un alto grado de simplicidad a las ecuaciones de la teoría y, junto con las diversas simetrías locales, sigue un largo camino hasta dar una forma única a nuestro modelo estándar de las partículas elementales.
Un ejemplo aún más extraño lo proporciona la historia de los principios de simetría interna. En física estos principios imponen típicamente una estructura de familias en la lista de partículas posibles. Estas transformaciones contínuas de simetría actúan sobre la etiqueta de las partículas de un modo que es matemáticamente equivalente a la forma en que las rotaciones ordinarias en tres dimensiones actúan sobre los espines de las partículas como protones, neutrones o electrones transformándolas en partículas que son combinaciones de varias de ellas con probabilidades arbitrarias de ser un protón, un neutrón o un electrón.
Las transformaciones que actuan de forma continua, como las rotaciones en el espacio ordinario o la combinación de electrones y neutrinos en la teoría electrodébil, se denominan grupos de Lie. Existen unos grupos de Lie simples a partir de los cuales pueden construirse todos los demás combinando sus transformaciones. En 1960 Gell-Mann descubrió que uno de estos grupos de Lie simples SU(3) era exactamente el necesario para imponer a la multitud de partículas elementales una estructura de familias similar a la que se había descubierto experimentalmente. Uno de los grandes éxitos de la nueva simetría SU(3) fue predecir una nueva partícula para completar una de las familias que fue descubierta con la masa predicha.
Un principio de simetría es simplemente una afirmación de que algo se ve igual desde varios puntos de vista, como por ejemplo una esfera o el espacio vacío. Pero lo realmente importante no son las simetrias de las cosas, sino las simetrías de las leyes o principios de invariancia. En general, las leyes de la naturaleza son simétricas o invariantes respecto a la traslación y la rotación espacial o a la traslación temporal. El principio de relatividad de la teoría de la relatividad también es una simetría de la naturaleza. Cualquier principio de simetría es a su vez un principio de simplicidad. Si estas simetrías de las leyes de la naturaleza son importantes en física clásica, su importancia es aún mayor en mecánica cuántica.
Un electrón es idéntico a cualquier otro salvo en su energía, momento y espín. Estas magnitudes son las que caracterizan las formas en que la función de onda responde a transformaciones de simetría. La materia pierde así su papel central en física.
Hoy día se acepta generalmente que la única forma de combinar los principios de la relatividad especial y la mecánica cuántica es a través de una teoría cuántica de campos o algo muy similar. Este es precisamente el tipo de rigidez lógica que da su belleza a una teoría realmente fundamental: la mecánica cuántica y la relatividad especial son casi incompatibles, y su reconciliación en la teoría cuántica de campos impone poderosas restricciones a la forma en que las partículas pueden interaccionar mutuamente.
Una de estas restricciones es que se difumina la diferencia entre campos y partículas. Todo son campos y las partículas son manifestaciones o excitaciones de los campos allí donde su energía es suficiente para crearlas. Y en el caso de las partículas virtuales, ni eso porque gracias al principio de incertidumbre pueden tomar prestada la energía del vacío durante un tiempo suficientemente pequeño. De hecho así funcionan las interacciones, mediante el inintercambio de partículas virtuales.
En el caso del campo electromagnético, la interacción entre dos electrones es debida al intercambio de fotones y la interacción entre un electrón y un fotón por el intercambio de electrones (campo electrónico). La distinción entre materia y fuerza deja de ser esencial porque las partículas de materia también pueden transmitir fuerzas.
Otra de estas restricciones es que la energía y el momento de los campos esta cuantizada. Por ejemplo, en el campo gravitatorio la energía es transportada por los gravitones.
Todas las teorías mencionadas hasta ahora solamente limitan los tipos de fuerzas y materia que una teoría puede contener: en sí mismas no requieren la existencia de ningún tipo particular de materia o fuerza. Los principios de simetría se han vuelto cruciales en las últimas décadas del siglo XX: hay principios de simetría que dictan la existencia misma de todas las fuerzas conocidas de la naturaleza.
La simetría subyacente en la teoría electrodébil no es espacio-temporal sino que tiene que ver con la identidad de las partículas. En mecanica cuántica es posible tener una partícula que no es, por ejemplo, ni un electrón ni un neutrino hasta que no se mida una propiedad que las distinga como la carga eléctrica. En la teoría electrodébil, la forma de las leyes de la naturaleza permanece invariable si reemplazamos electrones y neutrinos por estados combinados de ambos.
Esta es la simetría que conecta las fuerzas electromagnéticas con las fuerzas nucleares débiles. El fotón y las partículas W± y Z aparecen en la teoría electrodébil como paquetes de energía de cuatro campos, campos que son requeridos por esta simetría de la teoría electrodébil de igual forma que el campo gravitatorio es requerido por las simetrías de la relatividad general.
Estas simetrías se denominan simetrías internas porque estan relacionadas con la naturaleza intrínseca de las partículas más que con su posición o movimiento. La invariancia de las leyes de la naturaleza bajo un grupo de tales transformaciones de simetría interna dependientes de la posición y el tiempo se denomina simetría local o gauge.
Es la simetría local entre diferentes sistemas de referencia en el espacio y en el tiempo lo que hace necesaria la gravitación y, análogamente, es una segunda simetría local entre electrones y neutrinos lo que hace necesaria la existencia del campo fotónico, del campo W y del campo Z.
Todavía existe una tercera simetría local exacta asociada con la propiedad interna de los quarks conocida como carga de color. Cada uno de los 6 tipos o sabores de quarks se da en tres colores: rojo, blanco y azul. Pues existe una simetría exacta de la naturaleza entre los diferentes colores. La fuerza entre un quark rojo y uno blanco es la misma que entre un quark blanco y uno azul, y la fuerza entre dos quarks rojos es la misma que entre dos quarks azules.
Pero esta simetría va más allá del mero intercambio de colores. En mecánica cuántica podemos considerar estados de un solo quark que no son ni exactamente rojos ni exactamente blancos ni exactamente azules. Las leyes de la naturaleza toman exactamente la mismisma forma si reemplazamos los quarks rojos, blanco y azul por quarks en tres combinaciones de estados apropiada.
El hecho de que las leyes de la naturaleza no se vean afectadas al variar de un lugar a otro y de un instante a otro hace necesario incluir en la teoría una familia de campos que interaccionan con los quarks, análogos al campo gravitatorio. Son ocho campos que se conocen como campos gluónicos. La teoría de tales fuerzas, la cromodinámica cuántica, es sencillamente la teoría de quarks y gluones que respeta esta simetría de color local. El modelo estándar de las partículas elementales consiste en la teoría electrodébil ccombinada com la cromodinámica cuántica.
No solo los principios de simetría dan una especie de rigidez o inevitabilidad a las teorías. Únicamente con estos principios la teoría electrodébil o la cromodinámica cuántica serían solo uno de los muchos tipos de teorías posibles. La restricción adicional que nos permite escoger nuestro modelo estándar sencillo de entre la variedad de teorías más complicadas que satisfacen los mismos principios de simetría es que sea renormalizable. Resulta que esta condición impone un alto grado de simplicidad a las ecuaciones de la teoría y, junto con las diversas simetrías locales, sigue un largo camino hasta dar una forma única a nuestro modelo estándar de las partículas elementales.
Un ejemplo aún más extraño lo proporciona la historia de los principios de simetría interna. En física estos principios imponen típicamente una estructura de familias en la lista de partículas posibles. Estas transformaciones contínuas de simetría actúan sobre la etiqueta de las partículas de un modo que es matemáticamente equivalente a la forma en que las rotaciones ordinarias en tres dimensiones actúan sobre los espines de las partículas como protones, neutrones o electrones transformándolas en partículas que son combinaciones de varias de ellas con probabilidades arbitrarias de ser un protón, un neutrón o un electrón.
Las transformaciones que actuan de forma continua, como las rotaciones en el espacio ordinario o la combinación de electrones y neutrinos en la teoría electrodébil, se denominan grupos de Lie. Existen unos grupos de Lie simples a partir de los cuales pueden construirse todos los demás combinando sus transformaciones. En 1960 Gell-Mann descubrió que uno de estos grupos de Lie simples SU(3) era exactamente el necesario para imponer a la multitud de partículas elementales una estructura de familias similar a la que se había descubierto experimentalmente. Uno de los grandes éxitos de la nueva simetría SU(3) fue predecir una nueva partícula para completar una de las familias que fue descubierta con la masa predicha.
La Simetría como Origen de la Ecuación Maestra
Para llegar a la ecuación maestra los artífices del Modelo Estándar impusieron condiciones de simetría. Intuyeron que la naturaleza es simétrica.
Si manipulamos una ecuación mediante una transformación concreta y esta no varía, entonces dicha transformación se corresponde con una simetría.
Existen simetrías del espacio-tiempo como el principio de relatividad, la traslación en el tiempo, la traslación en el espacio o la rotación espacial. Estas simetrías anteriores son también globales. Pero también existen simetrías internas (locales) que cumplen los campos.
Una de ellas es la simetría gauge, consistente en variar la fase del campo en cada punto de manera independiente. Para que la ecuación resultante no varíe se añade un campo que se transforme de la manera apropiada para que la ecuación se mantenga invariable. Ese campo añadido es el correspondiente a la partícula portadora de la interacción. Por ejemplo, en el caso del fotón sería el campo electromagnético, que aparece al imponer la simetría gauge a la ecuación de Dirac.
Por ejemplo, partimos de la ecuación de Dirac para una partícula libre (sin interacciones). Es decir, la primera línea de la ecuación maestra. Si ahora imponemos la simetría gauge, nos aparecen gratis la segunda, la tercera y la cuarta líneas. La simetría gauge hace aparecer las tres interacciones y sus partículas mediadoras.
Ecuación de Dirac que se obtiene de la lagrangiana de Dirac (la primera línea de la Ecuación Maestra). Las constantes de Planck y de la velocidad de la luz se han igualado a la unidad
Ecuación de Dirac para una dimensión espacial escrita de forma más explícita
Pero no solo eso. La simetría gauge hace que no tengamos más que la opción de la ecuación maestra. Nos conduce inexorablemente hacia ella.
Esta simetría es una propiedad de las ecuaciones subyacentes en el modelo estándar, pero esta simetría no es satisfecha por las soluciones de dichas ecuaciones, es decir, por las propiedades de las propias partículas. Por eso los bosones W± y Z tienen masa pero el fotón no. Igual pasa con el electrón y el neutrino. Las masas concretas de estas partículas son una situación particular de las ecuaciones. La simetría de las ecuaciones no está necesariamente reflejada en cada solución individual de dichas ecuaciones, sino solo en el conjunto total de todas las soluciones de las ecuaciones. La naturaleza tal como la conocemos es sólo una solución de todas las ecuaciones del modelo estándar, y no supone ninguna diferencia qué solución sea con tal de que todas las diferentes soluciones estén relacionadas mediante principios de simetría exacta.
En tales casos decimos que la simetría está rota. Llamamos a este fenómeno una ruptura espontánea de simetría porque nada rompe la simetría en las ecuaciones de la teoría. La ruptura de simetría aparece espontáneamente en las diversas soluciones de estas ecuaciones. Hay mas simetría y belleza en las leyes de la naturaleza de lo que parece por simple observación. Un ejemplo de simetría rota es un imán, que por debajo de 770° desarrolla un campo magnético en cierta dirección aunque las ecuaciones que lo gobiernan son espacialmente simétricas.
En el caso de la teoría electrodébil existe una ruptura espontánea de simetría que se manifiesta en una diferencia de masa entre el fotón y los bosones W± y Z que a su vez hace que la intensidad y el alcance de ambas difiera.
La teoría electrodébil está basada en un principio de simetría exacta, que dice que las leyes de la naturaleza son invariantes si en sus ecuaciones reemplazamos los campos del electrón y del neutrino por campos combinados de ambos, y al mismo tiempo combinamos análogamente los campos de las otras familias de partículas como el quark up y el quark down. Este principio de simetría es local porque estas combinaciones pueden variar con la posición y el tiempo.
Los campos del fotón y de los bosones W± y Z son una familia de campos cuya existencia viene dictada por una simetría similar a la que impone el campo gravitatorio por la simetría entre diferentes sistemas de coordenadas. Estos campos también deberían combinarse entre sí al combinar los campos del electrón y del neutrino y los campos de los quarks. Por eso la simetría entre electrones y neutrinos es también una simetría entre las fuerzas electromagnética y nuclear débil.
Acoplamiento entre los tres bosones gauge débiles
Esta simetría es una propiedad de las ecuaciones subyacentes en el modelo estándar, pero esta simetría no es satisfecha por las soluciones de dichas ecuaciones, es decir, por las propiedades de las propias partículas. Por eso los bosones W± y Z tienen masa pero el fotón no. Igual pasa con el electrón y el neutrino. Las masas concretas de estas partículas son una situación particular de las ecuaciones. La simetría de las ecuaciones no está necesariamente reflejada en cada solución individual de dichas ecuaciones, sino solo en el conjunto total de todas las soluciones de las ecuaciones. La naturaleza tal como la conocemos es sólo una solución de todas las ecuaciones del modelo estándar, y no supone ninguna diferencia qué solución sea con tal de que todas las diferentes soluciones estén relacionadas mediante principios de simetría exacta.
En tales casos decimos que la simetría está rota. Llamamos a este fenómeno una ruptura espontánea de simetría porque nada rompe la simetría en las ecuaciones de la teoría. La ruptura de simetría aparece espontáneamente en las diversas soluciones de estas ecuaciones. Hay mas simetría y belleza en las leyes de la naturaleza de lo que parece por simple observación. Un ejemplo de simetría rota es un imán, que por debajo de 770° desarrolla un campo magnético en cierta dirección aunque las ecuaciones que lo gobiernan son espacialmente simétricas.
En el caso de la teoría electrodébil existe una ruptura espontánea de simetría que se manifiesta en una diferencia de masa entre el fotón y los bosones W± y Z que a su vez hace que la intensidad y el alcance de ambas difiera.
Pero la simetría gauge exige que ninguna de las partículas del Modelo Estándar tenga masa, lo cual es erróneo, pues implicaría que todas las partículas se moverían a la velocidad de la luz. Tampoco podemos renunciar a las simetrías que tan elegantemente y correctamente hacen aparecer las tres interacciones. Es más, sin ella la teoría carece de sentido.
Si consideramos la aproximación de que todas las partículas tienen mada nula (ello implica que se mueven a la velocidad de la luz y no pueden estar nunca en reposo), entonces se manifiesta la similitud entre los bosones de las tres interacciones. La teoría electrodébil y la QCD tienen una estructura matemática semejante, perteneciendo ambas a las llamadas teorías gauge o de Yang-Mills.
Cuando también se asigna masa nula a los fermiones, aparecen muchas simetrías entre las tres familias, mostrando idénticas propiedades.
El Campo de Higgs
El primer término de la quinta línea indica la generación de masa de las partículas elementales (LYukawa) y la última línea indica la generación de masa de los bosones gauge débiles W+, W- y Z° (LHiggs). En esta última línea la letra griega φ indica el campo de Higgs.
La aproximación de masa nula
Si consideramos la aproximación de que todas las partículas tienen mada nula (ello implica que se mueven a la velocidad de la luz y no pueden estar nunca en reposo), entonces se manifiesta la similitud entre los bosones de las tres interacciones. La teoría electrodébil y la QCD tienen una estructura matemática semejante, perteneciendo ambas a las llamadas teorías gauge o de Yang-Mills.
Cuando también se asigna masa nula a los fermiones, aparecen muchas simetrías entre las tres familias, mostrando idénticas propiedades.
Sin embargo esto no se da en la realidad con lo que necesitamos un mecanismo que asigne la gran variedad de masas de las partículas conocidas sin eliminar las simétrias.
El Campo de Higgs
La solución está en las dos últimas líneas de la ecuación maestra que describen el Mecanismo de Higgs y la ruptura espontánea de la simetría electrodébil. Las masas se generan como consecuencia de la interacción de las partículas con el campo de Higgs.
A la izquierda el potencial de Higgs es nulo cuando el campo de Higgs también lo es. Sin embargo a la derecha se rompe esta simetría y el potencial es diferente de cero cuando el campo de Higgs es nulo, lo que acaba proporcionando masa a los bosones gauge débiles
Parte de la ecuación maestra que describe la generación de masa de las partículas elementales y de los bosones gauge débiles
Ruptura espontánea de simetría
La ruptura espontánea de simetría rompe la aproximación de masa nula mediante la existencia de un nuevo bosón: el bosón de Higgs.
Una diferencia importante entre el bosón de Higgs y los fermiones y bosones conocidos previamente es que debe tener espín nulo a diiferencia de los fermiones que tienen espín semientero (los del modelo estandar ½) o de los bosones, que tienen y entero.
La esencia de este mecanismo es que las ecuaciones con una simetría determinada pueden tener soluciones que violen individualmente esa simetría, aunque el conjunto de todas las soluciones sea simétrico.
Por ejemplo si tenemos un lápiz en equilibrio (inestable) vertical sobre una mesa, el sistema tiene simetría pues el lápiz puede caer potencialmente en cualquier dirección. En el momento de caer, la simetría se rompe porque la dirección en la que el lápiz cae ya no es equivalente al resto.
Igual sucede con un conjunto de imanes orientados aleatoriamente (existe simetría pues todas las direcciones son equivalentes). En el momento en que dos imanes se orientan espontaneamente en la misma dirección poco a poco todos los imanes se orientan paralelamente quedando todos apuntando en la misma dirección y rompiendo la simetría.
La mayor virtud de este mecanismo es que permite que los fermiones y los bosones gauge débiles adquieran masa no nula evitando los infinitos en la teoría electrodébil.
La ruptura espontánea de simetría de la fuerza electrodébil se debe a la presencia de un campo cuyo valor de vacío es no nulo. Es este valor diferente de cero lo que hace que la simetría se rompa. Como todos los campos cuánticos, la energía y el momento de este nuevo campo viene en paquetes, el bosón de Higgs.
A la izquierda el potencial de Higgs es nulo cuando el campo de Higgs también lo es. Sin embargo a la derecha se rompe esta simetría y el potencial es diferente de cero cuando el campo de Higgs es nulo
Con la inclusión del campo de Higgs todas las partículas tienen masa nula salvo el bosón de Higgs, cuya masa es la única que aparece en el modelo estándar. Todas las demás partículas adquieren una masa proporcional al bosón de Higgs mediante el mecanismo de ruptura espontánea de la simetría electrodébil. Por tanto conocer el origen de la masa sería equivalente a entender el mecanismo de ruptura espontánea de simetría. Es posible que en el origen del universo la simetría electrodébil no estuviera rota, y que se rompiera pocos instantes después al bajar la temperatura de un umbral.
Valor no nulo del Campo de Higgs en el vacío
Al principio el Campo De Higgs tenía un valor nulo. Pero poco después del Big Bang, este campo tomó un valor no nulo debido a una transición de fase provocada por la bajada de la Temperatura. El enfriamiento del Universo (reducción de su energía) era entonces insuficiente para mantener la simetría.
Cuando el Universo se enfrió, un vacío sin el campo de Higgs era una configuración energética menos favorable que un vacío lleno de bosones de Higgs, que era el estado natural. En ese momento se produce la Ruptura Espontánea de la Simetría Electrodébil. Sin este fenómeno, los electrones no tendrían masa, se moverían a la velocidad de la luz con lo que no se hubieran podido formar los átomos, de ahí la importancia del Mecanismo de Higgs.
El descubrimiento de Higgs salva la validez del Modelo Estándar, la teoría que describe el mundo subatómico y vigente desde principios de la década de los 70. Aunque esta teoría realiza gran cantidad de predicciones acertadas, no es capaz de explicar el origen de la masa de las partículas si no es mediante el bosón de Higgs. Si este bosón no se descubriera, el Modelo Estándar carecería de coherencia interna y habría que corregirlo o buscar una nueva teoría que lo sustituyera.
El Origen de la Masa
Las partículas elementales deben poseer masa (energía por existir). Sin embargo es muy difícil incorporar consistentemente una masa no nula para las partículas en el Modelo Estándar de Partículas sin estropear otros hechos básicos, como ciertas simetrías que sabemos que se cumplen. El bosón de Higgs y el Mecanismo de Higgs pueden solucionarlo.
El solenoide compacto de muones es un detector de partículas ubicado bajo tierra, en una gran caverna excavada en las instalaciones del Gran Colisionador de Hadrones. Este detector ayudará en la búsqueda del bosón de Higgs y en la adquisición de nuevos conocimientos acerca de la naturaleza de la materia oscura
Las propiedades de las interacciones y sus partículas mediadoras son consecuencia de las simetrías del Modelo Estándar. Es más, las propias interacciones son consecuencia de estas simetrías.
No obstante estas simetrías implican que las masas de las partículas mediadoras debe ser nula, lo que ocurre para el fotón, el gravitón y el gluón pero no para los bosones gauge débiles W+, W-, y Z°. A su vez la ausencia de estas simetrías puede provocar inconsistencias en el Modelo Estándar. Necesitamos que las ecuaciones sean simétricas con lo que la masa de las partículas debe ser nula. Esta inconsistencia hacía peligrar el Modelo Estándar completo.
¿Cómo reconciliar pues las simetrías de las interacciones con la masa de las partículas? La respuesta es mediante el Mecanismo de Higgs, una manera elegante de solucionar esta aparente inconsistencia, y posiblemente la más sencilla. Por eso los científicos tenían tanta confianza en que lo acabarían encontrando.
En la propuesta de Higgs, el campo de Higgs impregna el espacio como si de un líquido viscoso se tratara haciendo que las partículas que interaccionan con él adquieran masa al friccionar con él y experimentar resistencia al movimiento.
Este mecanismo conserva la simetría y se solucionan las inconsistencias. A pesar de la masa, la simetría sigue estando ahí, aunque camuflada. El Campo de Higgs permite que las simetrías se rompan "aparentemente". La simetría permanece en las ecuaciones, pero no en las soluciones.
La diferencia de masa entre las partículas viene por la intensidad diferente de interacción de la partícula con el Campo de Higgs. Desafortunadamente el mecanismo de Higgs dice por qué las partículas tienen masa pero no cuánto debe valer, a excepción de los bosones gauge débiles. Los valores de estas masas han sido confirmados por experimentos en el CERN.
La Ruptura Espontánea de Simetría permite que las partículas mediadoras de las interacciones asociadas a las simetrías rotas adquieran masa. Igual que todas las partículas de la materia al interaccionar con el Campo de Higgs. Las simetrías que se rompen son las relacionadas con las interacciones cuyos bosones tienen masa, es decir, los bosones gauge débiles.
La interacción débil y la electromagnética provienen de una gran simetría, la llamada electrodébil. Esta simetría se camufla debido a que el Campo de Higgs es no nulo en el vacío. Sin embargo no toda la simetría se rompe porque los fotones no tienen masa al no interaccionar con el bosón de Higgs.
El proceso mediante el cual se rompe espontáneamente la simetría de la fuerza débil es el mecanismo de Higgs. Para que el mecanismo de Higgs rompa espontáneamente la simetría de la fuerza débil, tiene que haber una partícula con una masa aproximadamente igual a la masa de la escala débil, que es 250 GeV (recuérdese que la relatividad especial relaciona la masa y la energía mediante la fórmula E=mc2).
El origen de la masa
En las teorías cuánticas de campos las partículas pueden desintegrarse o saltar de un punto a otro. ¿Cuál es pues el origen de la masa? La explicación actual radica en el mecanismo de Higgs y el bosón de Higgs.
Las partículas se mueven por todos las caminos posibles, el directo y mediante zigzagueos (contracciones que son proporcionales al inverso de la masa). Si la masa es nula, la contracción es infinita con lo que el zigzagueo es imposible, quedando solo el camino directo (regla de salto de partículas con masa nula). La cantidad de zigzagueo es lo que interpretamos como masa.
La interacción con el bosón de Higgs origina el zigzagueo y la aparición de la masa. El fotón no tiene ninguna regla de desintegración que lo acople a las partículas de Higgs, por ello no interactúan con él y no tienen masa.
La mecánica cuántica con el principio de incertidumbre afirma que no existe el espacio vacío porque entonces la energía sería definida y precisa, sino un frenesí de creación de partículas y antipartículas dentro de lo permitido por el principio de incertidumbre. Por eso no es extraño suponer que el espacio vacío pueda estar impregnado de bosones de Higgs.
Las partículas de Higgs surgieron de una transición de fase que se produjo muy poco tiempo después del Big Bang al reducirse la energía por debajo de un umbral.
Cuando el Universo se enfrió, un vacío sin bosones de Higgs era una configuración energéticamente menos favorable que un vacío lleno de partículas de Higgs, que era el estado natural.
En el caso de protones y neutrones el mecanismo de Higgs es poco importante porque su masa es fundamentalmente la energía de los gluones y pares quarks-antiquarks. Sin embargo, es importante para explicar el origen de la masa de los bosones gauge débiles W y Z.
Importancia del Bosón de Higgs
El descubrimiento de Higgs salva la validez del Modelo Estándar, la teoría que describe el mundo subatómico y vigente desde principios de la década de los 70. Aunque esta teoría realiza gran cantidad de predicciones acertadas, no es capaz de explicar el origen de la masa de las partículas si no es mediante el bosón de Higgs. Si este bosón no se descubriera, el Modelo Estándar carecería de coherencia interna y habría que corregirlo o buscar una nueva teoría que lo sustituyera.
Ruptura de la simetría temporal
El mecanismo de Higgs puede ser también responsable de la pequeña desviación de la simetría de inversión temporal observada en la física de partículas. Esta ruptura sería otro ejemplo de ecuación simétrica con un conjunto simétrico de soluciones asimétricas, de las cuales solo una se observa en la naturaleza. En este caso habría dos soluciones, que difieren en el sentido del tiempo.
Ruptura de la simetría materia-antimateria
Si se combinan las operaciones matemáticas que intercambian el sentido del tiempo, con la que intercambia derecha e izquierda y con la que intercambia materia y antimateria, la operación resultante, llamada simetría CPT es una simetría exacta de la teoría cuántica de campos.
Por ello la ruptura espontánea de la simetría temporal supone también la ruptura de simetría entre materia y antimateria. ¿Podría esta ruptura ser la responsable de que apenas haya antimateria en nuestro universo?
El concepto de ruptura espontánea de simetría también se ha utilizado para intentar incluir la fuerza nuclear fuerte dentro del mismo marco unificado que las fuerzas débil y electromagnética. Sin embargo no existe una simetría en las ecuaciones del modelo estándar que relacionen las fuerzas nucleares fuertes con la débil y la electromagnética.
Por desgracia, la razón de que la gravitación quede fuera del modelo estándar es que resulta muy difícil describir la gravitación en el lenguaje de la teoría cuántica de campos. Podemos aplicar simplemente las reglas de la mecánica cuántica a las ecuaciones de campo de la relatividad general, pero entonces entramos en el viejo problema de los infinitos. Por ejemplo se obtienen probabilidades infinitas en lo que sucede en colisiones de dos gravitones que intercambian más de un gravitón.
El problema de la jerarquía
El valor tan elevado de la energía de Planck nos enfrenta a otro gran problema. Esta energía surge en un nivel tan profundo que podemos suponer que es la unidad fundamental de energía que aparece en las ecuaciones de la teoría final. El misterio está en por qué todas las demás energías son tan pequeñas. La masa del bosón de Higgs se estima 100 billones de veces más pequeña que la energía de Planck. Esto significa que hay una jerarquía de simetrías: cualquiera que sea la simetría que unifica las fuerzas gravitatoria y nuclear fuerte con las fuerzas electrodébiles se rompe aproximadamente 100 billones de veces más fuertemente que la simetría que unifica las interacciones débiles y electromagnéticas. Esto se conoce como el problema de la jerarquía. Otra forma de plantear el problema de la jerarquía consiste en preguntar por qué la gravedad es tan débil, tan poco intensa en relación con las otras fuerzas no gravitatorias.
Aunque sepamos que el mecanismo de Higgs es el responsable de las masas de las partículas, el ejemplo conocido más sencillo que implementa el mecanismo de Higgs funciona solamente con un apaño muy grande. En la teoría más sencilla uno esperaria que las masas de los bosones gauge débiles y de los quarks fueran aproximadamente diez mil billones de veces más grandes de lo que son. El problema de la jerarquía es la cuestión de por qué esto no es así.
Una aproximación a este problema se basa en la supersimetría, una nueva simetría que relaciona partículas de diferente espín de modo que forman nuevas «superfamilias». En estas teorías la masa del bosón de Higgs sería nula en las ecuaciones fundamentales de la teoría y aparecería a partir de un complicado mecanismo de ruptura de la supersimetría.
Más allá del problema de la jerarquía, la conjetura de que todas las fuerzas de la naturaleza se unificarán a una energía del orden de la energía de Planck ha arrojado una nueva luz sobre el problema de los infinitos. La condición de renormalización fue una poderosa guía para la construcción del modelo estándar. Pero como el modelo estándar deja fuera la gravitación, se cree que es simplemente una aproximación válida a baja energía a una teoría unificada realmente fundamental y que pierde su validez a energías como la energía de Planck. Por eso el problema de los infinitos no ha desaparecido, sino que es un problema para la teoría final, no para una aproximación a baja energía como parece ser el modelo estándar.
Podría ser que las ecuaciones del modelo estándar no son del tipo muy simple que sería renormalizable, sino que contienen cualquier término concebible consistente con las simetrías de la teoría. Estos nuevos términos no renormalizables aparecerían divididos por potencias de alguna cantidad del orden de la energía de Planck, que a bajas energías serían despreciables. La condición de renormalización era correcta a efectos prácticos aunque no lógicamente necesaria.
Estos nuevos términos hacen que algunas magnitudes no se conserven, como la del número de quarks o el número leptónico. La primera impide la desintegración del protón en un positrón y un fotón y garantizaría la estabilidad de la materia. La segunda hacía que el neutrino tuviera masa nula. Experimentos como el super Kamiokande de Japón han mostrado que los neutrinos tendrían una masa minúscula con lo que no se conservaría el número leptónico. Esto hace que el neutrino pueda mutar de un tipo a otro (electrónico, muónico y tau) y explicaría por qué históricamente siempre se había detectado menos neutrinos del primer tipo de los esperados procedentes del Sol.
El origen de la QED está en la cuantización del campo electromagnético de Maxwell por Dirac en los años 20. La QED explica:
¿Cómo emite un electrón un fotón cuando se mueve entre los niveles de energía de un átomo?
¿Qué le sucede al fotón cuando es absorbido por un electrón?
¿Cómo las partículas con carga eléctrica interactúan entre sí y con las partículas de luz (fotones)?
La teoría cuántica antigua no explicaba por ejemplo el efecto Lamb, un ligero desplazamiento de los niveles de energía del hidrógeno debido a la emisión y absorción de fotones virtuales.
La QED lo explica todo salvo la gravedad y los fenómenos nucleares. Es decir, explica la materia, la luz, la electricidad y el magnetismo.
Antimateria
La QED permite a las partículas viajar hacia adelante y hacia atrás en el tiempo. Esto parece violar la ley de la causalidad pero puede interpretarse como una antipartícula viajando hacia adelante en el tiempo.
Las antipartículas fueron introducidas por Dirac en 1931 para explicar la existencia de partículas con energía negativa.
La teoría cuántica de campos es el nombre de la estructura matemática más profunda en la que se basan las reglas sobre los saltos y las desintegraciones, y destaca por ser la única teoría posible de las partículas diminutas que también respeta la relatividad especial. El aparato teórico de la teoría cuántica de campos obliga a fijar las reglas sobre saltos y desintegraciones, perdiendo la libertad de elegir otras nuevas.
Se utilizan simetrías para eliminar opciones, con lo que parece que el universo deba ser como es. Por ejemplo, la relatividad impone simetrías a la estructura del espacio-tiempo.
Finalmente el efecto Lamb no puede explicarse con la teoría cuántica de Heisenberg y Schrödinger. Solo los cálculos que consideran efectos de segundo orden como creaciones de parejas electrón-positrón como consecuencia de un fotón predicen correctamente los niveles de energía del átomo de hidrógeno.
El efecto Lamb fue el primer caso explicado con las fluctuaciones cuánticas. Actualmente la QED es la precursora de las teorías cuánticas de campos, es modelo de las teorías de las interacciones fuerte y débil.
Modelo Estándar
Las partículas conocidas se dividen en quarks (6 sabores agrupados en 3 familias cada uno de tres posibles colores), leptones (3 electrones y 3 neutrinos agrupados también en tres familias). Estas partículas forman la materia ordinaria conocida. Además tenemos los bosones mediadores de fuerzas como los fotones, gluones y los bosones gauge débiles W+- y Z. No sabemos porque son estas partículas las que son ni por qué las reglas son las que son. Estas reglas son una consecuencia de los principios de las teorías cuánticas de campos y de la simetría gauge.
Las principales diferencias entre las descripciones cuánticas de las distintas fuerzas tienen que ver con las reglas de desintegración. Con estas nuevas reglas podremos dibujar diagramas de Feynman y nos permitirán calcular la probabilidad de que se produzca algún suceso. Algunas de estas nuevas reglas son:
- Diagramas de Feynman de interacción de electrones con bosones gauge débiles W y Z.
- Diagramas de Feynman de interacción de quarks u y d con bosones gauge débiles W (importante para la fusión nuclear).
- Diagramas de Feynman de interacción entre gluones.
Respecto a la fuerza nuclear fuerte se cumple:
- Solo los quarks pueden descomponerse en gluones (además es lo más probable que suceda). Por eso es una fuerza nuclear fuerte.
- Tiene un alcance corto porque los gluones se desintegran rápidamente al interactuar con otros gluones. Los fotones alcanzan largas distancias porque no interactúan entre sí.
Renormalización del Modelo Estándar
El modelo estándar se distingue de la teoría de la gravitación por una propiedad extraordinaria llamada renormalización. Esto significa que puede separarse de la teoría unificada sin que aparezcan infinitos.
El precio a pagar es la aparición de más de una docena de parámetros arbitrarios, que no pueden calcularse teóricamente y deben ser determinados experimentalmente.
Estos parámetros representan la dependencia del modelo del resto de la teoría fundamental unificada, incluyendo el infinito conjunto de partículas de masa alta.
Otros infinitos aparecieron en otros cálculos y durante cuatro décadas fue el mayor obstáculo para el progreso de la física. Finalmente este problema se solucionó en teorías de cierto tipo especial, las renormalizables, sirviendo de criba para las teorías candidatas a una teoría final.
Acción
Esta magnitud es útil y una manera elegante de formular la mecánica clásica gracias al principio de mínima acción. Pero con la llegada de la mecánica cuántica paso de ser útil a esencial. Sus unidades son de energía por tiempo, igual que la constante de Planck.
Definición de la magnitud física llamada acción como la integral temporal del lagrangiano
El principio de mínima acción nos dice que las ecuaciones de movimiento surgen de minimizar una magnitud física llamada acción
Las ecuaciones de Euler-Lagrange obtenidas mediante el cálculo de variaciones proporcionan el lagrangiano L que minimiza la acción
El valor de la acción determina la probabilidad de cada una de las historias posibles para un suceso en mecánica cuántica.
A partir de esta lagrangiana y de la formulación de la integral de camino o de suma de historias de la mecánica cuántica propuesta por Richard Feynman pueden obtenerse las ecuaciones que gobiernan la evolución en el espacio-tiempo para un sistema cuántico.
Formulación de la integral de camino o de suma de historias de la mecánica cuántica propuesta por Richard Feynman
Según esta formulación de las historias posibles, la probabilidad de que una partícula cuántica vaya de (x,t) a (x',t') se calcula no considerando un único camino como en la mecánica clásica, sino los infinitos caminos que unen (x,t) con (x',t').
Cada camino tiene una contribución a la probabilidad total que es proporcional a eiLdt/2πh, siendo Ldt=S su acción correspondiente de forma que se suman las contribuciones de los infinitos caminos posibles y se eleva al cuadrado dicha suma para obtener la probabilidad total.
Todas las partículas elementales conocidas, salvo el gravitón, están descritas provisionalmente por la teoría del Modelo Estándar. Esta teoría parece estar en excelente acuerdo con la observación. Parece una buena teoría porque ha extraído mucha simplicidad de una gran variedad de fenómenos. Sin embargo, hay motivos por los que no puede ser la teoría definitiva de las partículas elementales:
- Las fuerzas se tratan como diferentes y no unificadas a pesar de que deberían ser muy similares y aparecer como diferentes manifestaciones de una misma fuerza subyacente.
- El modelo no es suficientemente simple. Distingue más de sesenta clases de partículas elementales sin explicar el motivo de tanta variedad.
- Contiene más de una docena de constantes arbitrarias no impuestas por la teoría que describen las masas de las partículas y las interacciones entre ellas.
- La gravitración no está incluida en el modelo y todos los intentos para incorporarla topan con dificultades desastrosas e infinitos.
Si el modelo estándar tiene gran poder predictivo, ¿por qué los físicos teóricos están tan tristes?
Los motivos son varios:
- El modelo estándar describe únicamente tres de las cuatro fuerzas conocidas dejando fuera la gravedad. Existen grandes obstáculos matemáticos para incorporarla en las teorías cuánticas de campos.
- La fuerza nuclear fuerte aparece de una forma bastante diferente de las fuerzas electromagnética y debil.
- Aunque el modelo estándar trata de forma unificada las fuerzas electromagnética y débil, existen diferencias obvias entre ambas como, por ejemplo, en su intensidad.
Muchas características del modelo estándar no están dictadas por principios fundamentales, sino que deben ser tomadas de la experiencia. Estas características aparentemente arbitrarias incluyen:
- una lista de partículas.
- ciertas constantes numéricas como las razones entre sus masas.
- las propias simetrías.
Por todo ello el modelo estándar claramente no es la respuesta final. Todos estos problemas del modelo estándar tienen que ver con la ruptura espontánea de simetría. El descubrimiento de este fenómeno ha sido uno de los grandes desarrollos liberadores de la ciencia del siglo XX. Su mayor éxito fue la explicación de las diferencias entre la fuerza electromagnética y la fuerza nuclear débil.
Actualmente existen varias preguntas a las que el modelo estándar no puede dar respuesta:
- ¿Por qué existen los campos que existen y no más o menos?
- ¿Por qué estos campos tienen las propiedades supuestas en el modelo estándar?
- ¿Por qué la naturaleza obedece los principios de la relatividad y de la mecánica cuántica?
- ¿Por qué la estructura de la materia se replica en tres generaciones de quarks y leptones?
- ¿Por qué todas las fuerzas se deben a simetrías gauge locales?
Las teorías de nueva física se centran sobretodo en obtener más conocimiento sobre:
- La Naturaleza del Bosón de Higgs.
- El Problema de la Jerarquía.
- El Misterio del Sabor y los Neutrinos.
- La Materia Oscura y la Energía Oscura.
- Gravedad Cuántica.
Estas teorías deberían darnos respuestas a preguntas como:
- ¿Por qué la materia elemental aparece en forma de partículas?
- ¿Por qué las masas de las partículas son las que son?¿Por qué los electrones tienen masa?
- ¿Por qué la materia se presenta en una estructura de 3 familias concretamente?
- ¿Por qué cada familia tiene masas mayores que la anterior?


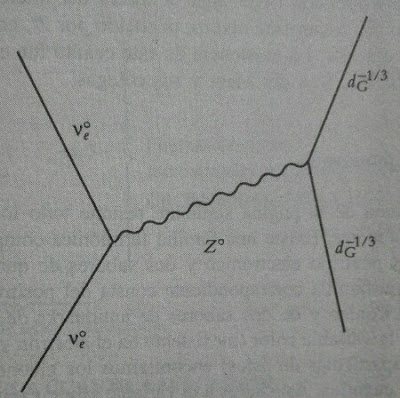

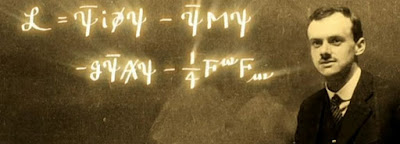



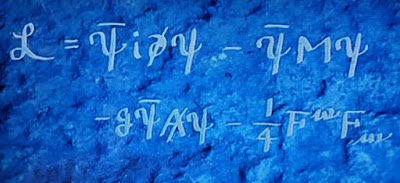













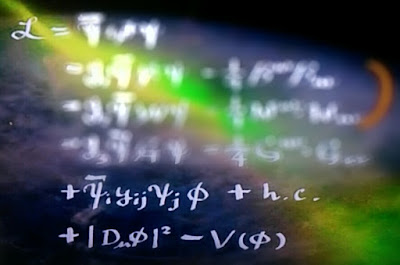





No hay comentarios:
Publicar un comentario